[영어] 수학 연산용어, 영어로: "제곱근 or 로그"
[미국영어] 수학 연산용어, 영어로: "제곱근 or 로그" 에 대해 리뷰하려고 합니다.
수학 연산에서 고급 단계는 지수 및 N차 루트 함수인데, 기본적인 연산용어를 정리해 보았네요.
지수 및 루트는 고급 개념이면서, 그래프 함수로 이해하면, 좀 더 활용하기 쉬워지는 것 같습니다.
지수 Exponent
지수 Exponent 는 기본 숫자가 자체와 몇 번 곱해지는지를 나타내는 수학적 표기법으로, 기본 숫자의 오른쪽에 지수가 위치하는데, 지수는 기본을 자체와 몇 번 곱할지를 나타냅니다. 지수가 2인 경우 기수 Base를 제곱하는 것을 나타내며, 3인 경우 기수를 세 번 곱하는 것을 표시합니다.
제곱근 Square Root
숫자의 제곱근 Square Root 은 자체와 자체를 곱했을 때 원래 숫자가 되는 값입니다. 루트 기호 (√)로 나타냅니다.
예를 들어 9의 제곱근은 3이며, 3×3=9 으로, 0 이상의 수에 대한 양수 및 음수 제곱근이 존재하며, 일반적으로 주로 사용되는 것은 양수 제곱근입니다.
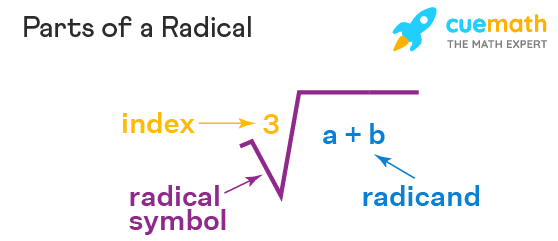
N차 루트 Nth Root
루트 Root 는 지수의 역연산을 나타내는 일반적인 개념입니다. 만약 n-번째 루트를 가정한다면, 일반적으로 지수를 통해 나타낼 수 있는데, n-번째 루트를 표시합니다.
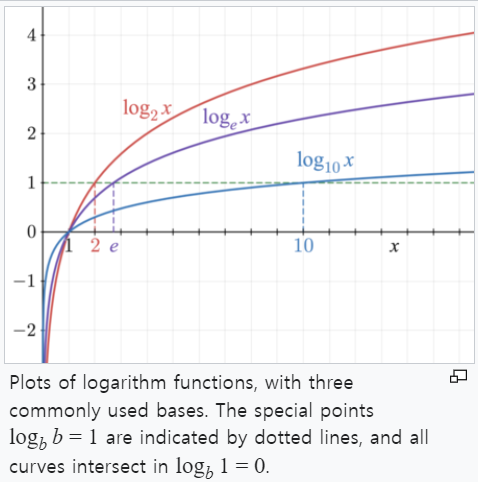
로그 Logarithm
로그 Logarithm 는 지수 연산의 역연산입니다. 만약 지수함수 b x = n 로 나타내면, 이를 로그함수 log b (a)=x로 표기합니다. 로그는 지수 방정식으로 표시되는데, 로그의 일반적인 밑 Base 으로는 10(일반 로그)과 e (자연로그)가 있습니다.
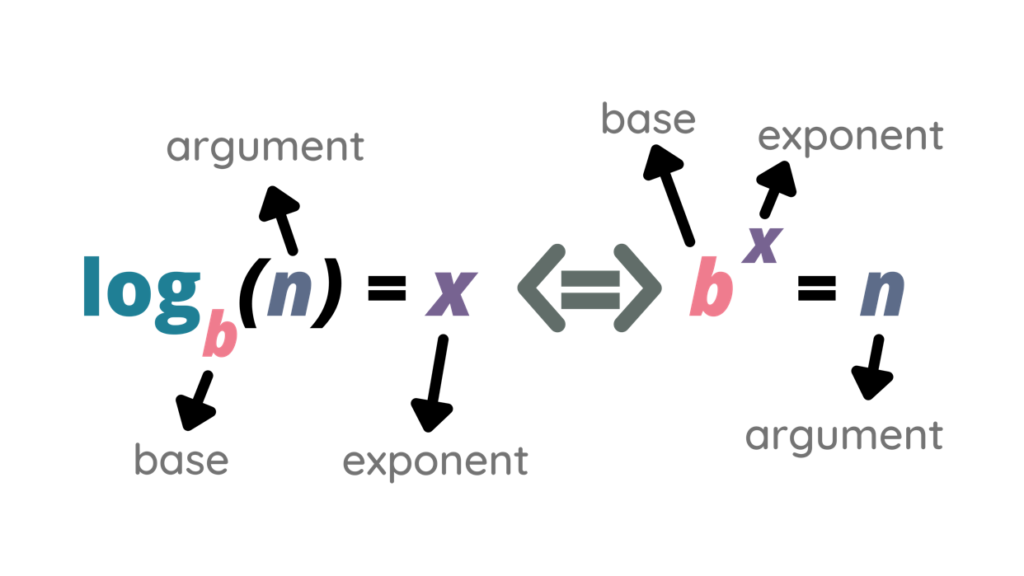
자연로그 Natural Logarithm
자연로그 Natural Logarithm 는 e를 밑으로 하는 로그로, ln(x)로 나타냅니다. 여기서 e는 오일러 수로 (약 2.71828) 나타낼 수 있는데, 자연로그는 주어진 수 x를 얻기 위해서 e가 몇 번 곱해져야 하는지를 나타냅니다.
자연로그는 주로 미적분학 및 수학적 분석을 포함한 다양한 수학 분야에서 사용되며 성장 및 감소 문제와 같은 다양한 분야에서 응용되네요.